Dado el buen recibimiento que tuvo el primer post, aquí va la continuación :D.
En este nuevo post hablaré, entre otras cosas, de las soluciones a los problemas propuestos al final de la parte 1. Sin embargo, no quiero ponerlos como un solucionario, sino que quiero explicar matemáticas usándolos.
Un Poco de Notación
No soy fan de introducir notación a menos que se justifique cuando recién se acaba de ver algo interesante, pero desafortunadamente tendré que cometer ese sacrilegio aquí.
En 2D hay 2 vectores bastante importantes
 y
y 
Esos los llamaremos 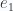 y
y  respectivamente, de esta manera ya tenemos una nueva forma de escribir vectores:
respectivamente, de esta manera ya tenemos una nueva forma de escribir vectores:

Para 3D también hay una notación análoga:
 ,
,  y
y 
Un posible problema aquí es que el mismo símbolo 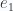 se usa para representar un vector en 2D y un vector en 3D; ante esta posible confusión, sólo nos queda confiar en que el contexto explique de qué
se usa para representar un vector en 2D y un vector en 3D; ante esta posible confusión, sólo nos queda confiar en que el contexto explique de qué 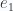 o de qué
o de qué  estamos hablando.
estamos hablando.
En algunos textos se utilizan las letras i, j y k para llamar a  respectivamente, pero esto tiene serios problemas:
respectivamente, pero esto tiene serios problemas:
- En dimensión mayor a 3 se vuelve confuso
- Con los números complejos la letra i representa un vector diferente:

- Con los cuaterniones la letra j y la letra k representan otros 2 vectores diferentes:
 y
y  .
.
- En la programación se suelen utilizar estas 3 letras para representar índices (recomendación: nunca llamen «j» a una variable, se confunde con la i).
Otra aplicación de esta notación, es que es posible recuperar las coordenadas de un vector sin necesidad de inventar funciones raras:
 representa la primera entrada(o coordenada x) de v
representa la primera entrada(o coordenada x) de v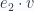 representa la segunda entrada(o coordenada y) de v.
representa la segunda entrada(o coordenada y) de v.
Ángulos
Como decía en la parte 1, es preferible usar vectores de dirección que usar ángulos directamente. El vector 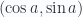 , es un vector de magnitud 1 de ángulo a; normalmente no es necesario conocer el valor de a, ya que por lo general usaremos siempre cos a y sen a en lugar de usar directamente el valor de a.
, es un vector de magnitud 1 de ángulo a; normalmente no es necesario conocer el valor de a, ya que por lo general usaremos siempre cos a y sen a en lugar de usar directamente el valor de a.
De igual manera, si queremos sumar ángulos podemos usar el producto complejo:

Ahora, hablando de propiedades importantes de los ángulos, quizá la que mas vamos a utilizar es que si dos vectores son ortogonales o perpendiculares, entonces su producto punto es 0, y además, si el producto punto de 2 vectores es 0 entonces son ortogonales.
Esta propiedad viene implícita en la interpretación geométrica del producto punto que vimos en la parte 1 (el producto de las magnitudes por el coseno).
De hecho esta propiedad es tan conveniente que ortogonal se define como producto punto igual a 0, por tanto, el vector (0,0) se considera que es ortogonal con todos los vectores del plano.
¿Qué son las Rectas?
Las rectas son un componente importante en la geometría y ya nos tardamos en abordarlas, así que ahora es el momento :).
Es común que la gente exprese las rectas usando ecuaciones tales como:

Hay que estar conscientes también de que a pesar de que todos hemos llegado a trabajar con ecuaciones de rectas, las rectas no son ecuaciones, ya que varias ecuaciones pueden representar la misma recta. Las rectas son todos los puntos que cumplen con las ecuaciones, es decir, las rectas son conjuntos.
Por ejemplo, la anterior ecuación representa este conjunto de puntos:
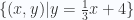
Lo cual se traduce como el conjunto de todos los puntos (x, y) tales que cumplen con esa ecuación.
La pregunta obligatoria es ¿qué clase de conjuntos son una recta? y ¿cómo expresar una recta a través de una fórmula?
En general no podemos definir las rectas a partir de ecuaciones con sólo escalares, ya que en 3D una ecuación con sólo escalares no determina una recta, sino un plano; necesitamos una definición que sirva tanto para 2D como para 3D y de ser posible, extensible a otras dimensiones.
La primer cosa a notar, es qué sucede con la multiplicación de un vector por un escalar:

Al multiplicar un vector por un escalar positivo, cambia su magnitud, incluso para cualquier vector a distinto de 0 y cualquier escalar 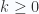 se cumple que
se cumple que  tiene magnitud k y la misma dirección que el vector a. Esto quiere decir que el conjunto de todos los multiplos por escalares positivos de un vector es una semirecta en la dirección del vector.
tiene magnitud k y la misma dirección que el vector a. Esto quiere decir que el conjunto de todos los multiplos por escalares positivos de un vector es una semirecta en la dirección del vector.
Con respecto a los múltiplos por escalares negativos, se obtendría una semirecta en dirección opuesta:

Es decir, una recta que pasa por el origen, es el conjunto de todos los múltiplos escalares de un vector.
Si tenemos una recta que pasa por el origen, es posible trasladarla sumándole un mismo vector a cada punto de la recta.
Dicho de otra manera:
 para
para 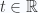 y
y  es un punto en la recta que pasa por el origen y que tiene la misma dirección que el vector D.
es un punto en la recta que pasa por el origen y que tiene la misma dirección que el vector D.
Mientras que  para
para 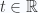 y
y 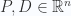 es un punto en la recta que pasa por P y que tiene la dirección D.
es un punto en la recta que pasa por P y que tiene la dirección D.
Por tanto, una manera de definir recta es la siguiente:
DEFINICIÓN: RECTA. Una recta r es un conjunto de puntos para los cuales existe un punto Q y un vector D, tal que |D|>0 y que:
 para algún escalar t
para algún escalar t 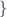
Esta definición sirve para 2D, 3D e incluso dimensiones más arriba.
Para propósitos de programación, lo mas sencillo es guardar el punto Q y el vector D.
TIP: Dados dos puntos A y B, la recta que pasa por ellos es:
{P | P=A+(B-A)t}
Intersección de Rectas
Primero que nada, es necesario resaltar que a pesar de que en 2D casi todas las rectas se intersectan, en 3D muy rara vez 2 rectas se intersectan; así que por el momento vamos a dejar el caso 3D a un lado y nos vamos a centrar en el 2D.
Tengo que admitir que por bastante tiempo yo me veía forzado a regresar temporalmente al uso de coordenadas y representaciones implícitas de rectas cada que quería encontrar el punto de intersección.
Sin embargo, luego aprendí un truco donde el producto cuña nos salva :D.
En la sección pasada se utilizó un hecho algebrárico, y es que el producto cuña de un vector consigo mismo siempre es 0 ; esto se deriva del hecho de que es antisimétrico, por tanto a^a=-a^a y el único número real que es su propio negativo es el 0.
Definiendo el problema, consideremos dos rectas r={P | P=A+Bt} y s={P | P=C+Dt}, queremos encontrar un punto que se encuentre en 2 rectas; lo cual es equivalente que hayar 2 números  y
y  tales que:
tales que:

Ahora, si encontramos sólamente  o sólamente
o sólamente  , no hay necesidad de encontrar el otro, y al mismo tiempo no queremos tener 2 incognitas en una misma ecuación, así que vamos a deshacernos de
, no hay necesidad de encontrar el otro, y al mismo tiempo no queremos tener 2 incognitas en una misma ecuación, así que vamos a deshacernos de  con la magia del producto cuña:
con la magia del producto cuña:

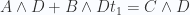
Luego de hacer esto ya se vuelve sencillo despejar  :
:

O de manera equivalente:
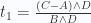
Nótese que esta solución sólo tiene sentido cuando  , y eso pasa cuando los vectores B y D no tienen la misma dirección; podría parecer una limitante, pero no lo es, ya que el producto cuña de B y D es 0 cuando el área del paralelogramo definido por (0, 0), B, D y B+D es 0, y eso sólo pasa cuando B y D tienen la misma dirección y si 2 rectas tienen la misma dirección entonces son paralelas y era de esperarse que el sistema de ecuaciones no tuviera solución,
, y eso pasa cuando los vectores B y D no tienen la misma dirección; podría parecer una limitante, pero no lo es, ya que el producto cuña de B y D es 0 cuando el área del paralelogramo definido por (0, 0), B, D y B+D es 0, y eso sólo pasa cuando B y D tienen la misma dirección y si 2 rectas tienen la misma dirección entonces son paralelas y era de esperarse que el sistema de ecuaciones no tuviera solución,
Proyecciones Ortogonales
Muchas veces tenemos 3 vectores  , (con a, b y c ortogonales entre sí) y queremos encontrar escalares
, (con a, b y c ortogonales entre sí) y queremos encontrar escalares  tales que:
tales que:

Este manera de sumar con pesos se le conoce como combinación lineal.
¿Ejemplos de cuándo es necesario hacer esto?
- En un FPS cuando el jugador presiona «W»(o cuando mueve el stick hacia adelante), el personaje no se mueve siempre en la misma dirección, sino que la dirección depende de hacia dónde esté mirando. Tampoco se mueve siempre en la dirección de la cámara, ya que puede estar mirando hacia arriba o hacia abajo pero siempre se debe de mover sobre el suelo. Algo que podría servir sería simplemente hacer 0 el eje Y, pero el suelo a veces está inclinado y también hay ocasiones en las que se desea trepar por el techo o las paredes, así que hacer 0 el eje Y no es una solución universal.
- La IA de un enemigo que intente esquivar un misil que se mueve en línea recta: necesita saber cómo está su posición con respecto a la recta por la que se mueve el misil, para saber si está a una distancia prudente de la recta o si se tiene que alejar, y también debe de saber cómo alejarse.
- Si una esfera cae al suelo con una velocidad v, y el suelo está inclinado, hay que encontrar un vector perpendicular al suelo y expresar la velocidad como combinación lineal de estos vectores.
De manera que el coeficiente del vector perpendicular al suelo es proporcional a qué tanto debe de rebotar la esfera, los otros coeficientes indican cómo aplicar la fricción.
- Como último ejemplo, si una esfera se está moviendo sobre el suelo con una velocidad v, si el suelo está inclinado entonces la gravedad modifica la velocidad de la esfera, para saber de qué manera la modifica es necesario expresar la gravedad como combinación lineal de los vectores de dirección del suelo y del vector perpendicular al suelo. Los coeficientes de los vectores de dirección indicarían hacia donde va a cambiar la velocidad la gravedad, mientras que el vector perpendicular al suelo es proporcional a la fricción.
Ahora volviendo al tema: ¿cómo expresar un vector como combinación lineal de otros vectores ortogonales?
La respuesta radica en la fórmula que vimos en la parte 1: 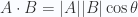 y un poco de trigonometria a la antigüa usanza. En particular tenemos la situación de esta imagen:
y un poco de trigonometria a la antigüa usanza. En particular tenemos la situación de esta imagen:

Al escalar  se le llama la proyección escalar de A sobre B, y al vector
se le llama la proyección escalar de A sobre B, y al vector  se le llama la proyección de A sobre B. Otra forma de expresar la proyección de A sobre B es multiplicando por |A| y dividiendo entre |A|, de esta manera no cambia su valor:
se le llama la proyección de A sobre B. Otra forma de expresar la proyección de A sobre B es multiplicando por |A| y dividiendo entre |A|, de esta manera no cambia su valor:

Usando la fórmula que vimos en la parte 1, la proyección se puede calcular así:

En general es preferible siempre proyectar sobre vectores de magnitud 1, ya que si B tuviera magnitud 1, podríamos calcular la proyección sin necesidad de dividir entre 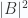 .
.
A estas alturas ya debería ser claro que la solución al problema planteado al inicio de la sección es:

Segmentos
Los segmentos de recta, o también llamados simplemente «segmentos», son líneas rectas que unen 2 puntos en el plano, O dicho de otra manera, si A y B son dos puntos, P está en el segmento que una a A con B, si P es colineal con A y con B y además P está entre A y B.
La primera parte(saber si P es colineal con A y con B) creo que ya la tenemos lo suficientemente clara, pero la segunda parte «P está entre A y B», aún hace falta aterrizarla.
SI estuviéramos hablando de números reales podríamos decir que P está entre A y B si A < P < B o si B < P < A; pero como estamos hablando de vectores, no podemos comparar así que necesitamos un sustituto para esto.
Una manera de hacerlo es observar que si A, B y P son colineales, entonces P-A y B-P van a ser un múltiplos escalares de B-A, si ambos son multiples escalares positivos, eso querría decir que tienen la misma dirección que B-A, lo que significaría que al moverse desde A hasta P y luego de P hasta B se sigue la misma dirección siempre.
Así que una definición mas aterrizada podría ser: P está en el segmento que une a A con B, si P es colineal con A y B; y además P-A y B-P tienen la misma dirección. Pero esta definición de segmento aún puede volverse más simple.
Recordemos que A+(P-A)+(B-P)=B, por tanto (P-A)+(B-P)=B-A, si P está en el segmento entonces P-A, B-P y B-A tienen exactamente la misma dirección, la cual llamaremos D, por lo cual existen escalares positivos j, k y m tales que:
P-A=jD, P-B=kD, y B-A=mD
Esto quiere decir que jD+kD=mD, lo cual es equivalente a:

Sustituyendo mD por B-A y m por |B-A|:

Esto implica que j+k=|B-A|, ya que ambos son positivos, así que  y
y 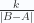 son números reales positivos que suman 1, lo cual quiere decir que existe un número entre 0 y 1 al que llamaremos t, tal que
son números reales positivos que suman 1, lo cual quiere decir que existe un número entre 0 y 1 al que llamaremos t, tal que 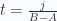 y que
y que 
De esta manera  , y después de ver todo esto, no es difícil convencerse de que cualquier t entre 0 y 1 que se elija, va a estar en el segmento, así que nuestra definición de segmento será la siguiente:
, y después de ver todo esto, no es difícil convencerse de que cualquier t entre 0 y 1 que se elija, va a estar en el segmento, así que nuestra definición de segmento será la siguiente:
El segmento de recta que une a A con B es el conjunto de puntos
{ P | P=A+(B-A)t para ![t\in [0,1]](https://s0.wp.com/latex.php?latex=t%5Cin+%5B0%2C1%5D&bg=fafcff&fg=2a2a2a&s=0&c=20201002) }
}
Esta definición trae explícito cual es el significado geométrico de A y de B, mientras que P es cada uno de los puntos del segmento, pero vale la pena pensar, ¿cuál es la relación entre P y t?
La relación entre P y t es la distancia entre P y A con respecto a la distancia entre A y B; es decir, |P-A|/|B-A|, si queremos partir el segmento en 3 segmentos de la misma longitud, lo haríamos elegiendo los valores 1/3 y 2/3 para t. Si queremos encontrar el punto que está a la mitad del segmento, basta con elegir t=0.5, de tal forma que P=A+(B-A)*0.5=(A+B)/2.
Si queremos saber si un punto P está en el segmento, podemos usar el producto punto de B-A y P-A, si el producto punto es exactamente igual a |B-A||P-A| (o muy cercano, en caso de que estemos programando y haya errores de precisión) eso querría decir que el coseno del ángulo entre los 2 vectores es 1, por tanto B-A y P-A tendrían la misma dirección y P estaría en la recta.
Una vez sabiendo que P está en la recta, para saber si está en el segmento, podemos usar la proyección orotogonal escalar de (P-A) sobre (B-A) y ver que sea menor que |B-A| y mayor que 0. Afortunadamente para nosotros, podemos reutilizar el mismo producto punto:
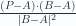
Distancia entre un Punto y una Recta
La distancia entre un punto P y una recta l se puede definir como la longitud del segmento mas corto que une un punto de l con P. Dicho segmento mas corto siempre forma un ángulo recto con l.

Es decir, la distancia entre el punto y la recta, sería |P-A|
Siendo l una recta, vamos a suponer que la tenemos representada a través de un punto Q y una dirección D:
l={B | B=Q+Dt} donde |D|=1
Hay que observar que A-Q es la proyección ortogonal del vector P-Q sobre el vector D.
Repasando, en este punto conocemos Q, conocemos D y conocemos P; por tanto podemos calcular P-Q; y dado que sabemos cómo hacer la proyección ortogonal, también podemos calcular A-Q, y por tanto podemos calcular A:
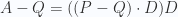
Lo que implica:
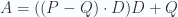
Dado que |P-A| es la distancia entre el punto y la recta, entonces la esta distancia se puede calcular así:

Significado Vectorial de la Representación Implícita de Rectas
A la representación de rectas como P=Q+tD se le llama representación explícita, mientras que a la representación por Ax+By+C=0 se le llama representación implícita. Estas denominaciones se deben a que la representación explícita dice cómo encontrar puntos de la recta(osea, sustituyendo valores de t), mientras que la implícita no dice eso, al menos no tan directamente.
Para explorar el significado vectorial de la representación implícita de rectas, veremos que pasa si en lugar de expresar la ecuación como una suma de productos, la expresamos como un producto punto:
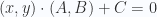
Sabemos que si la recta pasa por el origen, entonces
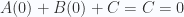
Esto quiere decir, que cuando una recta pasa por el origen, la ecuación expresada como producto punto toma esta forma:

Esto quiere decir, que (A, B) es un vector ortogonal a la recta.
Ahora, si la recta no pasa por el origen, entonces 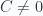 y el sistema de ecuaciones
y el sistema de ecuaciones
Ax+By+C=0
Ax+By=0
No tiene solución, por tanto, la recta correspondiente a la ecuación Ax+By+C=0 es paralela a la recta correspondiente con la ecuación Ax+By=0; lo cual implica que (A, B) es un vector perpendicular a la recta.
Ahora que ya tenemos significado geométrico tanto de A como de B, el único que nos falta es C.
Para encontrar este significado vamos a tomar el punto P=(x, y) de la recta más cercano al origen. Tenemos que el punto Q=P+(-B, A) también debe estar en la recta.
Ahora, consideremos el paralelogramo formado por los vértices 0, P, Q, y P+Q. Ya habíamos visto en la parte 1 que este paralelogramo tiene área 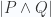 . Por tanto:
. Por tanto:

Es decir, el área del paralelogramo es |-Ax-By|, pero recordemos también que -Ax-By=C, por tanto, |C| es el área de ese paralelogramo.
Tenemos que la base de ese paralelogramo es el segmento que une al orígen con P, mismo que es la distancia de la recta al orígen, mientras que el segmento que une a P con Q es la altura del paralelogramo, y tiene longitud  , dado que el área del paralelogramo es igual al producto de la longitud de la base por la longitud de la altura, entonces la longitud de la base es:
, dado que el área del paralelogramo es igual al producto de la longitud de la base por la longitud de la altura, entonces la longitud de la base es:
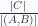
Misma que es la distancia de la recta al orígen.
Por tanto, ya sabemos el significado geométrico de C.
El Producto Complejo
El producto complejo es un producto exclusivo de  y se define de la siguiente manera:
y se define de la siguiente manera:
 para
para 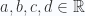
Este producto es conmutativo, asociativo y distributivo, y también tiene la propiedad de que el producto de 2 vectores es otro vector.
Una manera sencilla de recordar la definición de este producto es con el hecho de que 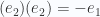 y
y  para cualquier vector v:
para cualquier vector v:

Lo cual es igual a:
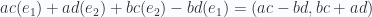
La interpretación geométrica de este producto es fascinante: Si  entonces |ab|=|a||b| y además la dirección de ab corresponde a la suma de los ángulos de a y de b, es decir:
entonces |ab|=|a||b| y además la dirección de ab corresponde a la suma de los ángulos de a y de b, es decir:

Para 
Lo cual significa que este geométricamente, este producto sirve para rotar y además tiene una gran propiedad algebrárica: es invertible. A grandes rasgos ser invertible quiere decir que es posible dividir, La forma de hacerlo es la siguiente:
 para
para 
Soluciones a Problemas de la Parte 1
A lo largo del texto mencioné entre párrafos maneras de solucionar la mayoría de los problemas, pero hubo unos cuantos problemas, que no encontré donde meterlos así que para cumplir lo prometido, aquí va una breve descripción(y poco de mala gana :S) de los problemas que faltaron:
- Dados los 3 vértices de un triángulo, encuentra una fórmula para saber su área.
El producto cuña da el área con signo del paralelogramo definido por (0, 0), A, B y A+B; el área del triángulo es la mitad de eso.
Por tanto si el triángulo tiene vértices A, B, C, el área del triángulo sería 
- Sobre las fórmulas de la longitud de las 3 alturas; si se quiere saber la longitud de la altura que pasa por un vértice C; simplemente se toman los otros 2 vértices del triángulo(llamémosles A y B), y vemos la distancia entre C y la recta que pasa por A y B:

- Dados 3 puntos A, P y Q, encontrar la reflexión de A sobre la recta que pasa por P y Q.
Esto se hace básicamente obteniendo la proyección B de A-Q sobre P-Q, de manera que Q+B sea el punto de la recta más cercano a A, y posteriormente sólo hay que sumarle a Q+B el negativo del vector A-(Q+B)
Q+B-(A-Q-B)=2(Q+B)-A, donde